In Part 1, I covered some oddities that sprouted from the mathematics of Quantum Mechanics. I also stated, with minimal explanation, that Einstein strongly argued against any hint of faster than light communication, and that if he were wrong about that and faster than light communication did exist, then there would be extremely dire consequences for the current state of science.
Investigating this is a perfect excuse to delve into the other half of mind-bending 20th century physics: Relativity.
The best starting point is how people naturally think the world works: the intuitive Newtonian world-view. In that scheme you can (in principle) accelerate forever and there is no universal speed limit. Newtonian time is also as we expect – past, present, and future. We can take snapshots of the present – maps, for example, show the world at a certain point in time. If we take a lot of maps we could turn them into a flip-book and see how things change (as in this informative example). Or, we can make a stack of the maps in chronological order, in which case the height of the stack is a representation of time.
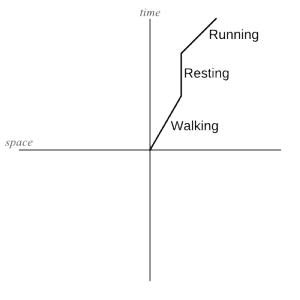
For this discussion, we don’t really care about the fact that space is three dimensional, so all that’s needed is time (vertical axis) and space (horizontal axis). The graph is then equivalent to either a one-dimensional universe with time, or merely ignores the other two dimensions of our three-dimensional world – either way, it’s now easy to graph on a flat screen. The picture on the right, above, shows a possible path through this graph. The ‘running’ section has a flatter slope because at a higher speed, our subject travels further in space (horizontally) per unit time (vertical) than when walking. When resting, the location does not change at all even as time progresses, and the path is vertical.
So with this graph in mind, we move to relativity, which is the logical conclusion of two axioms. One of them is this idea that the speed of light is the same for everyone, no matter where they are or what speed they’re moving. The question the name Relativity asks is ‘Relative to what?’ The answer is always ‘light’. The second is that physical laws work exactly the same, no matter how fast the experimenter is going.
The consequence of the first axiom is that light is the ultimate speed limit, c = 3•10^8 m/s. This is fast enough that any speed humans have familiarity with, everything seems Newtonian. The intuitive view is almost always good enough. But, according to Relativity, accelerating to c takes an infinite amount of energy, and would take an infinite amount of time at a constant acceleration – for anything with mass. Light, however, is massless, and massless objects have to move at the speed of light.
(This can be made intuitive very effectively, if somewhat improperly, by using the uncorrected, Pre-Relativity Newton’s Second Law: Force = Mass * Acceleration. Light has zero mass, so the rearranged equation gives: Force / 0 = Acceleration, which thanks to a division by zero suggests any force at all causes infinite acceleration. But, since c is the maximum in Relativity, infinite acceleration gives a final speed of c. That being said, onwards!)
Light being the absolute speed limit has some interesting side effects. Gravity, electromagnetism, all the forces that make things move are ALSO limited to the speed of light. As of the time of this writing, Mars is about 19 light-minutes away, which means we see it where it ‘was’ 19 minutes ago – and that the Earth feels it’s gravitational pull as being from where it ‘was’ as well. In short, ‘present’ is not horizontal, it’s bounded by the speed of light. Here’s a picture of the new space-time.
Those diagonal lines are light-paths, and are diagonal because light travels one light-year in one year – a slope of 1. Most non-astronomers don’t measure things by the speed of light, but it makes graphing Relativity very convenient, given that the speed of light is such a fundamental part of the theory. With a bit of thought, you can see that adding in another space dimension turns the light-speed lines of the ‘present’ into a cone. (The third spatial dimension turns the cone into a sphere which collapses to a point as time goes forwards, a four-dimensional cone.)
This picture shows teleportation, of the sort quantum entanglement collapse implied in Part 1. If orange and blue are two entangled particles, and the orange particle gets disturbed and collapses, then our observer’s right-angle-shaped ‘present’, sweeping forwards through time, will first see the blue particle collapse, and then see the orange particle getting prodded. The effect (blue particle collapsing) precedes the cause (orange particle collapsing).
Still, this does not seem so bad. The Blue and Orange collapses are still on the same horizontal plane as each other. Our observer might think it looks like they happened at different times, but that’s just because the speed of light is not infinite. Isn’t this actually the same nice neat horizontal layers of time as the chronological stack of Newtonian maps?
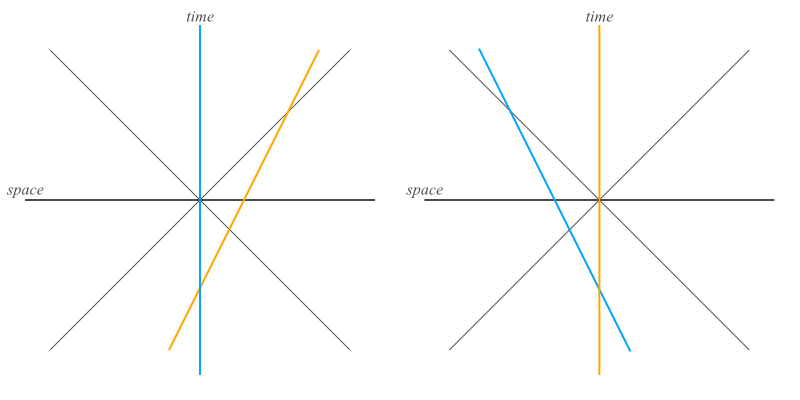
Well, no. Because the speed of light is constant for all observers, and the laws of the universe work the same way for all observers. That means that an observer sitting still and an observer on a very fast rocket both think they are on the vertical line of our graph. Below we have two diagrams of the exact same event.
If the blue line is Earth, and the orange line is a very fast space ship of some sort, then both of them see the other moving. Earth sees the spaceship moving forward at some speed, and the space ship sees Earth moving in the opposite direction at the same speed. The key part is that both Earth and the space ship are, to the best of their measurements, the vertical, unmoving line. That means they disagree on what the vertical line is.
However, since the speed of light is a constant, and everyone everywhere must agree on the speed of light, then the diagonal light-speed lines that both Earth and the ship see have to be the same. For the diagonal lines to be the same in the two graphs, AND for the vertical lines to be different, then the horizontal lines must ALSO be different for the two observers. What counts as one of the Newtonian time-slice ‘presents’ depends on the observer. This leads to our last picture, which shows the above situation along with the two observers’ two different ideas about what a slice of time is.
This one is a bit complicated, so first I have three observations about the chart that hopefully give you a better grasp of what is going on in it. Or, they might make it more confusing. If you get bogged down in any of them, the conclusion afterwards should still make sense.
- Both blue and orange have been given light-lines (in grey) – they both agree that light travels diagonally (one light-second distance in one second of time). Though, since blue and orange are some distance apart, a point can be in blue’s past but not yet in orange’s, or vice-verse.
- This picture describes the essence of the math I didn’t show – the Time and Space axes are mirrored around a light-speed diagonal. Yes, the blue lines here appear to be 45 degrees away, and the orange ones are around 17 degrees away from one of the lines and 73 degrees from the other, but the mirror symmetry is preserved in both cases, and always will be no matter what speeds are involved. This is, graphically, how the speed of light remains the same for all observers in Relativity.
- Finally, for an object going the speed of light the Time and Space axes would overlap each other – and with the diagonal light-speed line. It’s sort of an interesting question what that means. The answer involves a part of Relativity I haven’t mentioned at all so far: perception of time also changes depending on speed. Specifically, faster observers perceive time to be moving slower for them (or, equivalently, they see the flow of time for all ‘stationary’ objects to be passing faster). Having the two axes overlap means traveling in time and traveling in space occur at the same rate – the fastest rate possible, in fact. There is no time left over (so to speak) for anything to occur to the moving object – time stands still (and is perceived to be infinitely accelerated for everything else in the universe).*
So here’s the payoff. As shown earlier, teleportation of the sort Quantum Mechanics predicts is a horizontal line on these charts. So, let’s consider a teleportation between the center of the blue cross to the center of the orange ‘cross’. That’s a horizontal jump along the blue Space line, which is allowed. Now our teleported message/object/person is at the center of the orange cross.
Remember, from orange’s perspective, the orange cross is straight and the blue cross is crooked. Since physics works the same for both blue and orange, if blue can teleport along the blue Space axis, then Orange can teleport along orange’s Space axis.
So orange teleports the message back to blue, following the orange Space axis until it intersects the blue Time axis. You’ll notice that intersection of these two lines is BELOW (before, prior to!) the center of the blue cross where the message started. A single teleport didn’t break anything, but putting two teleportations together, one after the other, allows orange to respond to blue’s message before blue sent it. The conclusion is that allowing teleportation in Relativity opens the door to all sorts of irrational time-travel paradoxes that make the entire idea of cause and effect laughable. That’s why Einstein almost immediately discarded the possibility of Quantum Mechanical teleportation – it would make his entire theory of Relativity seem totally inconsistent with how the world seems to work.
Next: Two Theories in a Box
* Even further off topic, but one of the neater discoveries of modern physics: For a long time neutrinos were believe to be massless, like light. This hypothesis was discarded with much academic noise when it became apparent that neutrinos were changing their ‘flavor’ between being emitted by the sun and being detected on earth. For their properties to change, time had to have passed. For time to pass, neutrinos must have mass.
See Your Comment Here!